


Computational Geometry for Imprecise Data
Computational geometry deals with algorithms on geometric inputs.
Historically, geometric algorithms have focused on the ideal situation
in which an algorithm runs on a well-defined input and performs its
internal calculations using perfect precision. Note the two
simplifying assumptions in the previous statement: well-defined
input and perfect precision.
Luckily many geometric algorithms rely only on simple geometric
predicates that can be evaluated by determining the sign of a
low-degree polynomial so that the perfect precision assumed above can
be simulated by a fixed precision given as a function of the precision
of the input. In other cases, this is not so easy, but techniques
have been developed to allow robust geometric computation for a number
of problems and scenarios. These techniques are quite mature and
even appear in computational geometry libraries as ready-to-use
solutions.
The assumption of well-defined-input is the topic of the
current workshop. In many cases, geometric data comes from
measurements of continuous real-world phenomenon. In almost all
cases, the measuring devices used are subject to finite precision. In
such cases, the input data given to a geometric algorithm is only an
approximation of the real-world phenomenon. Applying a geometric
algorithm to this data can often be misleading since the output of
such algorithms is usually a combinatorial object such as a convex hull
or Delaunay triangulation. However, the structure of this object may
be deeply affected by the error in the input, and the actual structure
may be very different from that returned by the algorithm.
One solution to this problem is to design algorithms that explicitly
compute with imprecise data. This imprecise data can be modelled in
different ways. One possible model, for data that consists of points,
is to model each point as a region. This region represents all
possible locations for where the point might be. Given a collection
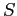 of such ``imprecise points'' one can then ask questions about
these points. What is their convex hull? What is their Voronoi
diagram/Delaunay triangulation?
of such ``imprecise points'' one can then ask questions about
these points. What is their convex hull? What is their Voronoi
diagram/Delaunay triangulation?
Of course, the exact structure of the convex hull/Voronoi
diagram/Delaunay triangulation depends on exactly where the points
are. However, it is possible to summarize the possible convex
hulls/Voronoi diagrams/Delaunay triangulations. For convex hulls, one
could classify each point as either definitely on the convex hull,
definitely not on the convex hull or uncertain. Similarly, a triple
of points could be definitely Delaunay, definitely not-Delaunay, or
possibly Delaunay. Alternatively, if one is concerned with a
worst-case outcome, it may make sense to consider optimization
problems on imprecise data. An example of such a question is: What is
the smallest (largest) area that the convex hull of 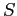 might have.
might have.
A related notion is that of robustness. When considering robustness,
the set 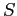 is a set of observed points. However, it is understood
that the observations that make up
is a set of observed points. However, it is understood
that the observations that make up 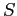 are subject to some (known or
unknown) level of accuracy. From
are subject to some (known or
unknown) level of accuracy. From 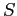 one computes a geometric
structure such as a convex hull as well as tolerances for (all
or part of) this structure. Such tolerances are usually expressed as
a value
one computes a geometric
structure such as a convex hull as well as tolerances for (all
or part of) this structure. Such tolerances are usually expressed as
a value 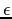 whose meaning is ``If no point of
whose meaning is ``If no point of 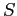 is more than
is more than
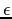 from its true location then this (part of the) structure is
correct.''
from its true location then this (part of the) structure is
correct.''
The remainder of this document contains a brief list of some of the
papers on the topic of computational geometry for imprecise data and
some papers to do with robustness and tolerance. Along with each
paper is a brief summary and/or copy of the paper's abstract.
Almost-Delaunay Simplices: Nearest Neighbor Relations for
Imprecise Points
Deepak Bandyopadhyay and Jack Snoeyink
download
Summary:The authors define almost delaunay simplices, which are sets of
points that could form delaunay simplices if all data points were
perturbed by at most 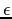 . They show that, for a given
. They show that, for a given
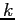 -simplex
-simplex 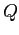 in a set
in a set 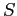 of points, finding the smallest value of
of points, finding the smallest value of
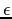 that makes
that makes 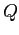 almost-delaunay is is equivalent to finding
the minimum-width annulus that contains
almost-delaunay is is equivalent to finding
the minimum-width annulus that contains 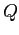 and whose interior sphere
is empty of points in
and whose interior sphere
is empty of points in 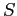 . They then propose and test algorithms
based on this observation.
. They then propose and test algorithms
based on this observation.
Delaunay Triangulations of Imprecise Points in Linear Time
after Preprocessing
M. Löffler and J. Snoeyink
download
Summary:We show how to preprocess a set of n disjoint unit disks in
the plane in O(n log n) time so that if one point per disk
is specified with precise coordinates, the Delaunay
triangulation can be computed in linear time. From the
Delaunay, one can obtain the Gabriel graph and a Euclidean
minimum spanning tree; it is interesting to note the roles
that these two structures play in our algorithm to quickly
compute the Delaunay.
Computing Delaunay Triangulation with Imprecise Input Data
A. A. Khanban and A. Edalat
download
Summary:The key step in the construction of the Delaunay triangulation
of a finite set of planar points is to establish
correctly whether a given point of this set is inside or
outside the circle determined by any other three points.
We address the problem of formulating the in-circle test
when the coordinates of the planar points are given only
up to a given precision, which is usually the case in practice.
By modelling imprecise points as rectangles, and
using the idea of partial disc, we construct a reliable
in-circle test that provides the best possible Delaunay
triangulation with the imprecise input data given by
rectangles.
We present a simple algorithm, which is 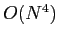 , but
illustrates the crucial role of the so-called in-circle
test in computing the Delaunay Triangulation.
, but
illustrates the crucial role of the so-called in-circle
test in computing the Delaunay Triangulation.
Guaranteed Voronoi Diagrams of Uncertain Sites
W. Evans and J. Sember
download
Summary:We investigate the Voronoi diagram that is induced by a
set of sites in the plane, where each site's precise
location is uncertain but is known to be within a particular
region, and the cells of this diagram contain those points
guaranteed to be closest to a particular site. We then
examine the diagram for sites with disc-shaped regions of
uncertainty, prove that it has linear complexity, and
provide an optimal O(n log n) algorithm for its construction.
We also examine the diagram for polygonal regions of
uncertainty, and prove that it has linear complexity as well.
We then describe a generalization of these diagrams, in which
each Voronoi cell is associated with a subset of the sites,
and each point in a cell is guaranteed to be closest to some
site in the subset associated with the cell.
Largest and Smallest Convex Hulls for Imprecise Points
Maarten Löffler and Marc van Kreveld
download
Summary:Assume that a set of imprecise points is given, where each point is
specified by a region in which the point may lie. We study the problem
of computing the smallest and largest possible convex hulls, measured
by length and by area. Generally we assume the imprecision region to
be a square, but we discuss the case where it is a segment or circle
as well. We give polynomial time algorithms for several variants of
this problem, ranging in running time from 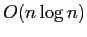 to
to 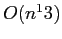 , and
prove NP-hardness for some other variants.
, and
prove NP-hardness for some other variants.
Approximating Largest Convex Hulls for Imprecise Points
Maarten Löffler and Marc van Kreveld
download
Summary:Assume that a set of imprecise points is given, where each point
is specified by a region in which the point will lie. Such a region
can be modelled as a circle, square, line segment, etc. We study the
problem of maximising the area of the convex hull of such a set. We
prove NP-hardness when the imprecise points are modelled as line
segments, and give linear time approximation schemes for a variety of
models, based on the core-set paradigm.
Computational Geometry with Imprecise Input Data
A. Edalat, A. Khanban, and A. Lieutier
download
Summary:The authors consider an imprecise input data model where each input
``point'' is represented as a convex polygon that includes the set of
all possible locations for that point. The output of an algorithm is
a pair of open sets that the interior and exterior of a partially
defined geometric object. In this model, the authors consider Voronoi
diagrams, Delaunay triangulations, and convex hulls. In the case
where the polygons have 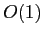 sides, these algorithms have
sides, these algorithms have 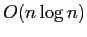 running times(?)
running times(?)
Efficient Indexing Methods for Probabilistic Threshold Queries
over Uncertain Data
Reynold Cheng, Yuni Xia, Sunil Prabhakar, Rahul Shah, Jeffrey Scott Vitter
download
Summary:In this applied paper, the authors consider the following scenario.
A set of data points
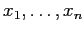 exist, where each
exist, where each 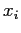 is a
random variable whose probability distribution is known. This data is
then processed so that it is possible to answer any
probabilistic threshold query
is a
random variable whose probability distribution is known. This data is
then processed so that it is possible to answer any
probabilistic threshold query 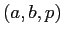 of the form:
Report all
of the form:
Report all 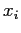 whose values are in the interval
whose values are in the interval ![$[a,b]$](img12.png) with probability at
least
with probability at
least 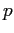 .
The authors show how to answer these queries using a variant of R-trees and give
experimental results. They also prove that this problem is at least
as hard as preprocessing for simplex range queries in 2D and halfspace
range queries in 3D.
.
The authors show how to answer these queries using a variant of R-trees and give
experimental results. They also prove that this problem is at least
as hard as preprocessing for simplex range queries in 2D and halfspace
range queries in 3D.
Querying Imprecise Data in Moving Object Environments
R. Cheng, D. V. Kalashnikov and S. Prabhakar
download
Summary:In this paper we study the execution of probabilistic
range and nearest-neighbor queries. The imprecision in
answers to queries is an inherent property of these
applications due to uncertainty in data, unlike the
techniques for approximate nearest-neighbor processing
that trade accuracy for performance. The notion of
probabilistic answers to queries over uncertain data
was introduced by Wolfson et al. for range queries,
where the answer consists of objects along with the
probability of each object lying in the query range.
We extend this idea to answer nearest-neighbor queries
– the answer consists of not a single object that is
closest to the object, but a set of objects each of
which have the potential of being the nearest neighbor
of the query point. In addition to identifying these
objects, the probability of each object being the
nearest neighbor can also be evaluated.
Engineering approach, no theoretical bounds.
Efficient Evaluation of Imprecise Location-Dependent Queries
J. Chen and R. Cheng
download
Summary:Studies the imprecise version of range queries. The query
returns the identities of all objects that fall within the
region. We propose efficient algorithms to compute
qualification probabilities. Moreover, we develop a set
of novel filtering techniques to determine quickly the
region which contains objects that may satisfy the query.
In particular, we classify a query according to whether the
location data being accessed is (1) precise (e.g.,
locations of gas stations, schools etc.), or (2) uncertain
(e.g., locations of moving objects).
Engineering approach, no theoretical bounds Also provide an
I/O efficient version.
Epsilon Geometry: Building Robust Algorithms from Imprecise Computations
L. Guibas, D. Salesin and J. Stolfi
download
Summary:We describe a new general framework, called Epsilon
Geometry, for coping with computational errors in geometric
algorithms that arise from the use of finite precision
arithmetic. The Epsilon Geometry framework allows us to build
robust geometric algorithms out of imprecise geometric
primitives. Our method combines the techniques of
interval arithmetic and backward error analysis, along
with a good deal of geometric reasoning. Our algorithms
compute an exact solution for a perturbed version of the
input, and they return a bound on the size of this implicit
perturbation.
Largest Bounding Box, Smallest Diameter,
and Related Problems on Imprecise Points
Maarten Löffler and Marc van Kreveld
download
Summary:We model imprecise points as regions in which one point must be
located. We study computing the largest and smallest possible values
of various basic geometric measures on sets of imprecise points, such
as the diameter, width, closest pair, smallest enclosing circle, and
smallest enclosing bounding box. We give efficient algorithms for most
of these problems, and identify the hardness of others.
Existence of Simple Tours of Imprecise Points
Maarten Löffler
download
Summary:Assume that an ordered set of imprecise points is given,
where each point is specified by a region in which the
point may lie. This set determines an imprecise polygon.
We show that it is NP-complete to decide whether it is
possible to place the points inside their regions in such
a way that the resulting polygon is simple. Furthermore,
it is NP-hard to minimize the length of a simple tour
visiting the regions in order, when the connections between
consecutive regions do not need to be straight line segments.
Agent Performance in Vehicle Routing when the Only Thing Certain is Uncertainty
Jordan Srour, Tamas Mahr, Rob Zuidwijk, and Mathijs de Weerdt
download
Summary:The authors consider a vehicle routing problem in which some fraction
of the requests are known in advance and some fraction arrive online.
The propose an agent-based solution for this problem and give
computational results for their solution.
This idea might lead to an interesting extension of online algorithm
and the competitive ratio to semi-online algorithms. For several
problems (paging, list organization, etc.) the (randomized and
deterministic) competitive ratio of these algorithms is
fully-understood. What effect does giving some of the access sequence
in advance have on the competitive ratio for these problems?
Computation with Imprecise Geospatial Data
Michael Worboys
download
Summary:Attempts to formalize imprecision in the context of GIS.
Basic Algorithms of Computational Geometry with Imprecise
Input (PhD Thesis)
Ali Asghar Khanban
download
Summary:This PhD thesis contains the results of some of Khanban's other papers
listed here.
Regular Polygons are Most Tolerant
William Evans
download
Summary:The author shows that a regular 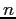 -gon is the most tolerant in the
sense that, among all convex
-gon is the most tolerant in the
sense that, among all convex 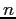 -gons, the regular
-gons, the regular 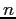 -gon requires
the largest perturbation of its vertices to make it non-convex. This
answers a question posed by Abellanas, Hurtado, and Ramos (1994).
-gon requires
the largest perturbation of its vertices to make it non-convex. This
answers a question posed by Abellanas, Hurtado, and Ramos (1994).
Geometry with Imprecise Lines
M. Löffler, M. van Kreveld
download
Summary:Proposes definitions for convex sets of lines(?)
Computational Geometry for Imprecise Data
This document was generated using the
LaTeX2HTML translator Version 2002-2-1 (1.71)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html -split 0 summaries
The translation was initiated by Pat Morin on 2008-11-30



Pat Morin
2008-11-30
![]() of such ``imprecise points'' one can then ask questions about
these points. What is their convex hull? What is their Voronoi
diagram/Delaunay triangulation?
of such ``imprecise points'' one can then ask questions about
these points. What is their convex hull? What is their Voronoi
diagram/Delaunay triangulation?
![]() might have.
might have.
![]() is a set of observed points. However, it is understood
that the observations that make up
is a set of observed points. However, it is understood
that the observations that make up ![]() are subject to some (known or
unknown) level of accuracy. From
are subject to some (known or
unknown) level of accuracy. From ![]() one computes a geometric
structure such as a convex hull as well as tolerances for (all
or part of) this structure. Such tolerances are usually expressed as
a value
one computes a geometric
structure such as a convex hull as well as tolerances for (all
or part of) this structure. Such tolerances are usually expressed as
a value ![]() whose meaning is ``If no point of
whose meaning is ``If no point of ![]() is more than
is more than
![]() from its true location then this (part of the) structure is
correct.''
from its true location then this (part of the) structure is
correct.''
![]() , but
illustrates the crucial role of the so-called in-circle
test in computing the Delaunay Triangulation.
, but
illustrates the crucial role of the so-called in-circle
test in computing the Delaunay Triangulation.