Planar Point Location

Slab Partitioning

Consider the planar subdivision, S in figure 1 below. Now take a vertical line form each vertex and extend it upwards and downwards to infinity. This extension partitions the plane into a set of vertical slabs. If we sort the vertical lines by x-coordinate then given a query point q we can determine in O(log n) time which slab that query point falls into. It is also possible, since all edges in S either do not cross, or completely cross, any slab to sort the crossing segments. Now we can also search in O(log n) time to determine which edges q falls between. Thus the planar point query becomes two O(log n) queries, and its therefore O(log n) itself. This method was originally proposed by Dobkin and Lipton (1976).

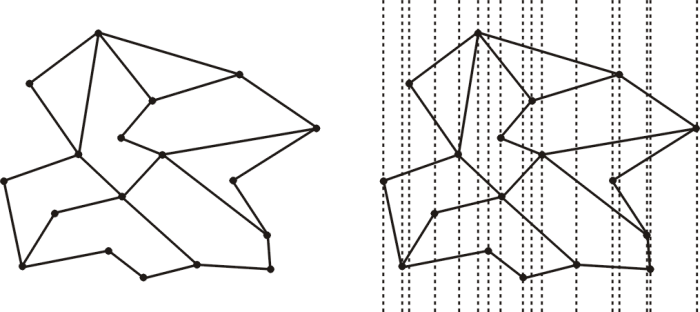
Fig. 1:A planar subdivision and its resulting slab partition.

Unfortunately the slab partitioning problem has a very serious drawback. Its storage requirement is worst case O(n²). Figure 2 shows a subdivision where such worst case behavior can occur.

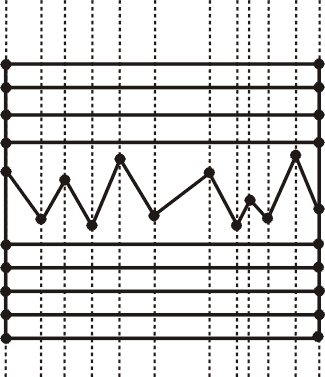
Fig. 2:A case where slab partitioning can result in O(n²) storage.

While slab partitioning does not provide an efficient solution to the planar point location problem due to the high storage requirements, if a better subdivision could be found with similar search properties but with lower storage requirements, this method is promising. Two such methods, that take different approaches will be presented in the following sections. First, Sarnak and Tarjan's use of persistent search structures which reduces the size of the search structure of slab partitioning to an 0(n), and secondly a slightly differing partitioning based on slab partitions, called a trapezoidal map will be discussed.